Post | RLG

1 变量含义

Frenet和Cartesian相互转换即 $[s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] \leftrightarrow[\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x]$
还要用到的中间变量有$\boldsymbol{n_x},\boldsymbol{t_x},\boldsymbol{n_r},\boldsymbol{t_r},\boldsymbol{r},d’,d^{\prime\prime},\theta_r,\Delta\theta,\kappa_r,\kappa_x’,\kappa_r’$
各变量含义：

变量	含义
$\boldsymbol{X}$	Cartesian坐标系下的坐标($\boldsymbol{X}=[x,y]$)
$\boldsymbol{r}$	trajectory上的点$\boldsymbol{X}$对应center line上最近点的Cartesian坐标
$v_x,a_x$	Cartesian坐标系下的速度和加速度
$s,\dot{s},\ddot{s}$	Frenet坐标系下的纵向坐标及其对时间的高阶导($\frac{d}{dt}$)
$s_x$	trajectory的弧长(注：centerline弧长$s_r$默认写成$s$)
$d,\dot{d},\ddot{d}$	Frenet坐标系下的横向坐标及其对时间的高阶导($\frac{d}{dt}$)
$d’,d^{\prime\prime}$	Frenet坐标系下的横向坐标对纵向坐标的高阶导($\frac{d}{ds}$)
$\theta_x,\theta_r$	Cartesian坐标系下trajectory/center line的切线与x轴的夹角
$\theta_r’$	$\theta_r’=\frac{d\theta_r}{ds_r}=\kappa_r$
$\Delta\theta$	$\Delta\theta = \theta_x - \theta_r$
$\boldsymbol{n_x},\boldsymbol{t_x}$	Cartesian坐标系下trajectory的法线和切线 $\boldsymbol{n_x}=[-\sin{\theta_x},\cos{\theta_x}]^T$ $\boldsymbol{t_x}=[\cos{\theta_x},\sin{\theta_x}]^T$
$\boldsymbol{n_r},\boldsymbol{t_r}$	Cartesian坐标系下center line的法线和切线 $\boldsymbol{n_r}=[-sin{\theta_r},\cos{\theta_r}]^T$ $\boldsymbol{t_r}=[\cos{\theta_r},\sin{\theta_r}]^T$
$\kappa_x,\kappa_r$	Cartesian坐标系下trajectory/center line的曲率
$\kappa_x’,\kappa_r’$	Cartesian坐标系下trajectory/center line的曲率对纵向坐标的导数($\frac{d}{ds}$)

2 推导

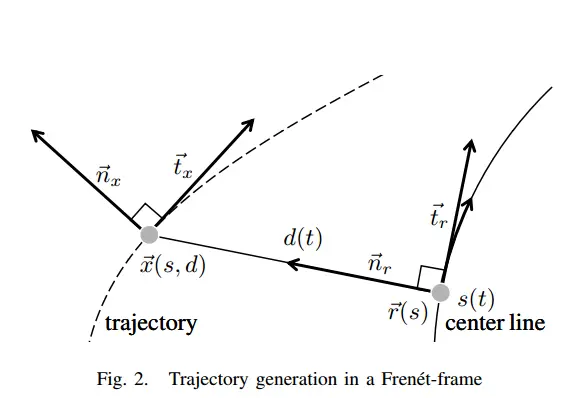
先来推导$\dot{d}$，由图像容易看出，$d=(\boldsymbol{x}-\boldsymbol{r})^T\boldsymbol{n_r}$，两边对t求导得： $$ \dot{d}=[\dot{x}-\dot{r}]^T\boldsymbol{n}_r+[x-r]^T\dot{\boldsymbol{n}}_r $$

$\dot{x}$很直观，$\dot{x}=v_x\boldsymbol{t_x}$，由[变化量很小时，弧长=割线=切线]的思想，$\dot{r}=\dot{s}\boldsymbol{t_r}$，最难求的是$\dot{\boldsymbol{n}}_r$，由于

$$\boldsymbol{n_r}=[-\sin{\theta_r},\cos{\theta_r}]^T$$

两边对时间求导，得到

$$\dot{\boldsymbol{n}}_r=[-\cos{\theta_r},-\sin{\theta_r}]^T\dot{\theta_r}=-\boldsymbol{t_r}\theta_r’\dot{s}=-\boldsymbol{t_r}\kappa_r\dot{s}$$

从而： $$ \begin{aligned} \dot{d}&=v_x\boldsymbol{t_x}^T\boldsymbol{n}_r-\dot{s}\boldsymbol{t_r}^T\boldsymbol{n}_r-[x-r]^T\boldsymbol{t_r}\kappa_r\dot{s} \\&=v_x\boldsymbol{t_x}^T\boldsymbol{n}_r \quad \quad \quad 注：\boldsymbol{t_r},\boldsymbol{n}_r正交;[x-r],\boldsymbol{t_r}正交 \\&=v_x[\cos{\theta_x},\sin{\theta_x}][-\sin{\theta_r},\cos{\theta_r}]^T \\&=v_x\sin{\Delta\theta} \end{aligned} $$

下面推导$d’$：

$$ d’=\frac{dd}{ds}=\frac{dd}{dt}\frac{dt}{ds}=\frac{\dot{d}}{\dot{s}}=\frac{1}{\dot{s}}v_x\sin{\Delta\theta} $$

要把未知量 $\dot{s}$消掉，通过$v_x$来消：

$$ \begin{aligned} v_x &= ||\dot{x}||_2=||\frac{d(\boldsymbol{r}+d\boldsymbol{n}_r)}{dt}||_2 \\&=\dot{s}\boldsymbol{t}_r+\dot{d}\boldsymbol{n}_r-d\boldsymbol{t_r}\kappa_r\dot{s} \\&=||[\boldsymbol{t_r},\boldsymbol{n_r}] \begin{bmatrix} 1-\kappa_rd & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} \dot{s} \\ \dot{d} \\ \end{bmatrix}||_2 \\&=\sqrt{(1-\kappa_rd)^2\dot{s}^2+\dot{d}^2} \\&=\sqrt{(1-\kappa_rd)^2\dot{s}^2+d’^2\dot{s}^2} \end{aligned} $$

代入可得：

$$ \begin{aligned} d’^2&=(\frac{1}{\dot{s}}v_x\sin{\Delta\theta})^2=[(1-\kappa_rd)^2+d’^2]\sin^2{\Delta\theta} \\&\downarrow \\ d’(1-\sin^2{\Delta\theta})&= (1-\kappa_rd)^2\sin^2{\Delta\theta} \\&\downarrow \\ d’&=(1-\kappa_rd)\tan{\Delta\theta} \end{aligned} $$

下面推导$d^{\prime\prime}$，

$$ \begin{aligned} d^{\prime\prime}&=\frac{d\frac{dd}{ds}}{ds}=\frac{dd’}{ds}=(-\kappa_r’d-\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}\frac{d\Delta\theta}{ds} \\&=-(\kappa_r’d+\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds}-\frac{d\theta_r}{ds}) \\&=-(\kappa_r’d+\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds_x}\frac{ds_x}{ds}-\kappa_r) \\&=-(\kappa_r’d+\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\frac{d\theta_x}{ds_x}\frac{ds_x/dt}{ds/dt}-\kappa_r) \\&=-(\kappa_r’d+\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\kappa_x\frac{v_x}{\dot{s}}-\kappa_r) \end{aligned} $$

需要把未知量 $\dot{s}$消掉，由$0=(x-r)^T\boldsymbol{t}_r$两边对时间求导：

$$ \begin{aligned} 0&=(\dot{x}-\dot{r})^T\boldsymbol{t}_r+(x-r)^T\dot{\boldsymbol{t}}_r \\0&=v_x\boldsymbol{t}_x^T\boldsymbol{t}_r-\dot{s}\boldsymbol{t}_r^T\boldsymbol{t}_r+(x-r)^T\boldsymbol{n}_r\kappa_r\dot{s} \\0&=v_x\cos{\Delta\theta}-\dot{s}(1-\kappa_rd) \\&\downarrow \\v_x&=\dot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}} \end{aligned} $$ 代入，得到： $$ d^{\prime\prime}=-(\kappa_r’d+\kappa_rd’)\tan{\Delta\theta}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}(\kappa_x\frac{1-\kappa_rd}{\cos{\Delta\theta}}-\kappa_r) $$ 由上上式也可以求得$\dot{s}$： $$ \dot{s}=v_x\frac{\cos{\Delta\theta}}{1-\kappa_rd} $$ 最后来求$\ddot{s}$，由$a_x=\dot{v}_x$：

$$ \begin{aligned} a_x&=\dot{v}_x=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}\frac{ds}{dt}\frac{d}{ds}\frac{1-\kappa_rd}{\cos{\Delta\theta}} \\ &=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2[(-\kappa_r’d-\kappa_rd’)\frac{1}{\cos{\Delta\theta}}+(1-\kappa_rd)\frac{1}{\cos^2{\Delta\theta}}\sin(\Delta\theta)\Delta\theta’] \\ &=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2\frac{1}{\cos(\Delta\theta)}[(-\kappa_r’d-\kappa_rd’)+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta’] \end{aligned} $$ 其中： $$ \Delta\theta’=\frac{d(\theta_x-\theta_r)}{ds}=\frac{d\theta_x}{ds_x}\frac{ds_x}{ds}-\kappa_r=\kappa_x\frac{v_x}{\dot{s}}-\kappa_r=\kappa_x\frac{1-\kappa_rd}{\cos\Delta\theta}-\kappa_r $$

3 Cartesian 转 Frenet

$[\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x],\theta_r,\kappa_r \rightarrow [s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}]$
s,d通过找最近点求得
$\dot{s}=v_x\frac{\cos(\Delta\theta)}{1-\kappa_rd},\Delta\theta=\theta_x-\theta_r$
$\ddot{s}=\frac{\cos(\Delta\theta)}{1-\kappa_rd}[a_x-\frac{\dot{s}^2}{\cos(\Delta\theta)}[(-\kappa_r’d-\kappa_rd’)+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta’]]$
$\kappa_r’=\frac{d^2\theta_r}{ds^2}$
$d’=(1-\kappa_rd)\tan{\Delta\theta}$
$\Delta\theta’=\kappa_x\frac{1-\kappa_rd}{\cos\Delta\theta}-\kappa_r,\kappa_x=\frac{d\theta_x}{dt}\frac{1}{v_x}$
$\dot{d}=v_x\sin(\Delta\theta)$
$\ddot{d}=a_x\sin(\Delta\theta)+v_x\cos(\Delta\theta)\dot{s}\Delta\theta’$

4 Frenet 转 Cartesian

$[s,\dot{s},\ddot{s},d,\dot{d},\ddot{d}] \rightarrow [\boldsymbol{X},\theta_x,\kappa_x,v_x,a_x] $
$\boldsymbol{X}=\boldsymbol{r}+\boldsymbol{n}_rd,\boldsymbol{n}_r=[-\sin(\theta_r),\cos(\theta_r)]^T$
$\theta_x=\theta_r+\arctan\frac{d’}{1-\kappa_rd},d’=\frac{\dot{d}}{\dot{s}}$
$\kappa_x=\frac{\cos^3\Delta\theta[d^{\prime\prime}+(\kappa_r’d+\kappa_rd’)\tan(\Delta\theta)]}{1-\kappa_rd}+\frac{\kappa_rcos\Delta\theta}{1-\kappa_rd},d^{\prime\prime}=\frac{d\frac{dd}{ds}}{ds}=\frac{d\frac{\dot{d}}{\dot{s}}}{ds}=\frac{\ddot{d}\dot{s}-\dot{d}\ddot{s}}{\dot{s}^3}$(由$d^{\prime\prime}$的式子得到)
$v_x=\dot{s}\frac{1-\kappa_rd}{\cos(\Delta\theta)},\Delta\theta=\theta_x-\theta_r$
$a_x=\ddot{s}\frac{1-\kappa_rd}{\cos{\Delta\theta}}+\dot{s}^2\frac{1}{\cos(\Delta\theta)}[(-\kappa_r’d-\kappa_rd’)+(1-\kappa_rd)\tan(\Delta\theta)\Delta\theta’]$
$\kappa_r’=\frac{d^2\theta_r}{ds^2}$