最优控制与规划
对于确定性的环境中,强化学习的目标函数可以写为:
$$\begin{aligned} &\max_{a_1,…,a_T} \sum_{t=1}^T r(s_t,a_t) \\ &\text{s.t.} \quad s_{t+1}=f(s_{t},a_{t}) \end{aligned} \tag{1}$$
上述问题就是给定初始状态,在模型已知的情况下,给出一系列的动作。
Cross Entroy Method (CEM)
这里我们首先假设动作是离散的。我们可以使用一些随机优化方法,例如 Cross-entropy method (CEM):
- 随机初始化一个方差较大的关于所有动作 $A$ 的高斯分布:$p(A)$,其中 $A$ 表示一个动作序列.
- 从 $p(A)$ 中采样得到一堆动作序列:$A_1,A_2,…,A_N$.
- 计算每个动作序列的目标值:$J(A_1),J(A_2),…,J(A_N)$.
- 从所有动作中挑选不错的M个样本:$A_i,…,A_j$.
- 你用 $A_i,…,A_j$ 重新拟合 $p(A)$,使 $p(A)$ 更倾向于输出回报更高的动作序列,并回到 b.
这种方法的一个优点是可以多进程并行计算,并且非常容易实现;缺点是,动作空间的维数不能太高、horizon不能太长并且这是一种开环的规划方法。
Linear Quadratic Regulator (LQR)
对于连续的动作空间与状态空间,上述方法就不管用了,下面介绍连续状态空间与动作空间下优化问题(1)的求解,为了与控制学科中的符号标记保持一致,我们将公式(1)改写为:
$$\begin{aligned} & \min_{u_1,…,u_T} \sum_{t=1}^T c(x_t,u_t) \\ & \text{s.t.} \quad x_t=f(x_{t-1},u_{t-1}) \end{aligned} \tag{2}$$
将约束条件放入目标函数有:
$$\min_{u_1,…,u_T} c(x_1,u_1)+c(f(x_1,u_1),u_2)+…+c(f(f(…),u_{T-1}),u_T) \tag{3}$$
我们首先考虑线性二次型系统,即 $f(x,u)$ 是线性函数,$c(x,u)$ 是二次函数,注意加粗的是矩阵,未加粗的是向量:
$$\begin{aligned} & c(x_t,u_t)=\frac{1}{2}\left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T \mathbf{C}_t \left[ \begin{matrix} x_t\\u_t \end{matrix}\right] + \left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T c_t \\ & f(x_t,u_t)=\mathbf{F}_t \left[ \begin{matrix} x_t\\u_t \end{matrix}\right]+f_t \end{aligned}$$
对于优化问题(3),我们首先保持 $u_1,u_2,…,u_{T-1}$ 不动,先把 $u_T$ 算出来,优化问题变为:
$$\min_{u_T} \quad \text{const} + \frac{1}{2}\left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T \mathbf{C}_t \left[ \begin{matrix} x_t\\u_t \end{matrix}\right] + \left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T c_t \tag{4}$$
$$\mathbf{C}_T= \left[ \begin{matrix} \mathbf{C}_{x_T,x_T} & \mathbf{C}_{x_T,u_T}\\ \mathbf{C}_{u_T,x_T} & \mathbf{C}_{u_T,u_T} \end{matrix} \right], \quad c_T=\left[ \begin{matrix} c_{x_T} \\ c_{u_T} \end{matrix} \right]$$
式中 const 代表二次函数的常数项,这个优化问题就是个无约束的二次优化问题,对目标函数求梯度,并令梯度为0解线性方程就行了。
$$Q(x_T,u_T)=\text{const} + \frac{1}{2}\left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T \mathbf{C}_t \left[ \begin{matrix} x_t\\u_t \end{matrix}\right] + \left[ \begin{matrix} x_t\\u_t \end{matrix}\right]^T c_t \tag{5}$$
$$\nabla_{u_T}Q(x_T,u_T)=\mathbf{C}_{u_T,x_T}x_T+\mathbf{C}_{u_T,u_T}u_T+c_{u_T}^T=0$$
有:
$$u_T=-\mathbf{C}^{-1}_{u_T,u_T}(\mathbf{C}_{u_T,x_T}x_T+c_{u_T})$$
$u_T$可简写为:
$$u_T=\mathbf{K}_T x_T+k_T \tag{6}$$
到此,优化问题(4)就解出来了,根据上面的公式,如果我们知道 $x_T$ 就能马上得到 $u_T$。$Q(x_T,u_T)$ 中 $u_T$ 就可以不需要存在了,我们将其写为值函数的形式:
$$V(x_T)=\text{const} + \frac{1}{2}\left[ \begin{matrix} x_t\\\mathbf{K}_T x_T+k_T \end{matrix}\right]^T \mathbf{C}_t \left[ \begin{matrix} x_t\\\mathbf{K}_T x_T+k_T \end{matrix}\right] + \left[ \begin{matrix} x_t\\\mathbf{K}_T x_T+k_T \end{matrix}\right]^T c_t $$
可将上式简写为:
$$V(x_T)= \text{const} + \frac{1}{2}x^T_T\mathbf{V}_{T}x_T+x^T_Tv_T \tag{7}$$
由于 $x_T$ 可以根据 $u_{T-1}$ 与动力学方程导出,因此根据 $u_{T-1},x_{T-1}$ 就能得到 $x_T$:
$$x_T=f(x_{T-1},u_{T-1})=\mathbf{F}_{T-1} \left[ \begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]+f_{T-1} $$
根据公式(6)和上式,显然这是一个动态规划问题。在算法层面我们可以递归求解它。
$$\begin{aligned} &u_T=\mathbf{K}_T x_T+k_T \\ &x_T=\mathbf{F}_{T-1} \left[ \begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]+f_{T-1} \\ &…\\ &u_2=\mathbf{K}_2x_2+k_2 \\ &x_2=\mathbf{F}_1 \left[ \begin{matrix} x_1\\u_1\end{matrix} \right] + f_1\\ &u_1=\mathbf{K}_1x_1+k_1 \end{aligned}$$
因此,优化问题(3)就能根据上面所示的公式,不停的迭代解决。
然而,这个情形只是针对有限horizon的情况,如果是无限horizon情况呢?
再次我们引入强化学习中:$Q(s,a)=r(s,a)+\gamma V(s’)$ 的动态规划思想,有:
$$Q(x_{T-1},u_{T-1})=\text{const} + \frac{1}{2}\left[ \begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]^T \mathbf{C}_{T-1} \left[ \begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right] + \left[ \begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]^T c_{T-1}+V(f(x_{T-1},u_{T-1})) \tag{8}$$
简化公式(8),得到:
$$Q(x_{T-1},u_{T-1})=\text{const}+\frac{1}{2} \left[\begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]^T \mathbf{Q}_{T-1} \left[\begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]+\left[\begin{matrix} x_{T-1}\\u_{T-1} \end{matrix}\right]^T q_{T-1} \tag{9}$$
$$\mathbf{Q}_{T-1}=\mathbf{C}_{T-1}+\mathbf{F}^T_{T-1}\mathbf{V}_T \mathbf{F}_{T-1} \\ q_{T-1}=c_{T-1}+\mathbf{F}_{T-1}^T\mathbf{V}_T f_{T-1} + \mathbf{F}^T_{T-1}v_T$$
继续解这个方程,得到:
$$u_{T-1}=\mathbf{K}_{T-1}x_{T-1}+k_{T-1} \\
\mathbf{K}_{T-1}=-\mathbf{Q}^{-1}_{u_{T-1},u_{T-1}}\mathbf{Q}_{u_{T-1},x_{T-1}}\\
k_{T-1}=-\mathbf{Q}^{-1}_{u_{T-1},u_{T-1}}q_{u_{T-1}} \tag{10}$$
因此,我们从T时刻循环计算公式(9)和(10),就能得到所得的最优动作序列。下面给出LQR算法:
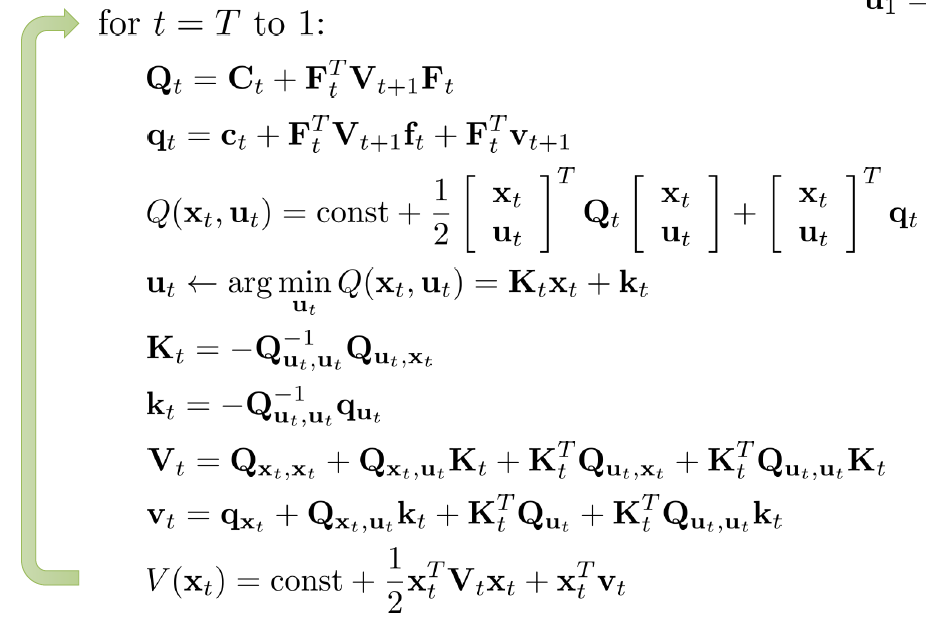
通过迭代计算,我们会得到一些列的 $\mathbf{K}_i$ 和 $k_i$,基于这些我们根据状态 $x_t$,就能得到对应的动作。
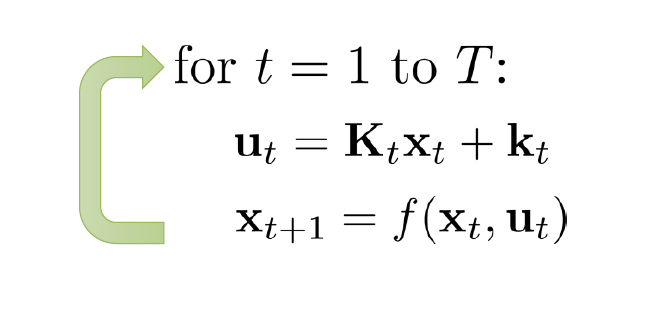
随机的动力学
以上 LQR 算法主要针对线性的确定的动力学系统,对于随机的环境(随机的不确定的动力学系统),我们可以在原有的确定的动力学系统上加上噪声。例如,对于线性系统:
$$f(x_t,u_t)=\mathbf{F}_t \left[\begin{matrix}x_t \\ u_t\end{matrix}\right] +f_t$$
其随机版本动力学可用高斯分布来描述:
$$x_{t+1} \sim p(x_{t+1}|x_t,u_t)\\
p(x_{t+1}|x_t,u_t)=\mathcal{N}\left(\mathbf{F}_t \left[\begin{matrix}x_t \\ u_t\end{matrix}\right] +f_t, \Sigma_t \right)$$
对于上述的LQR算法,只需将动力学过程修改为随机版本的动力学方程就行。
微分动态规划 (DDP/iterative LQR)
现在我们来考虑非线性系统的情形,对于 LQR,其动力系统是线性的,目标函数是二次函数。那么,对于非线性二次型系统,我们可以用泰勒展开对非线性系统的局部构建一个线性二次型系统。
$$f(x_t,u_t) \approx f(\hat{x_t}, \hat{u_t})+\nabla_{x_t,u_t}f(\hat{x_t},\hat{u_t})\left[\begin{matrix}x_t-\hat{x_t}\\u_t-\hat{u_t} \end{matrix}\right]$$
$$c(x_t,u_t)\approx c(\hat{x_t},\hat{u_t})+\nabla_{x_t,u_t}c(\hat{x_t},\hat{u_t})\left[\begin{matrix}x_t-\hat{x_t}\\u_t-\hat{u_t} \end{matrix}\right]+\frac{1}{2}\left[\begin{matrix}x_t-\hat{x_t}\\u_t-\hat{u_t} \end{matrix}\right]^T \nabla^2_{x_t,u_t} c(\hat{x_t},\hat{u_t})\left[\begin{matrix}x_t-\hat{x_t}\\u_t-\hat{u_t} \end{matrix}\right]$$
那么执行一个动作后,动力系统以及目标函数的增量为:
$$\overline{f}(\delta x_t,\delta u_t)=\nabla_{x_t,u_t}f(\hat{x_t},\hat{u_t}) \left[ \begin{matrix} \delta x_t\\ \delta u_t \end{matrix} \right]$$
$$\overline{c}(\delta x_t,\delta u_t) =\frac{1}{2}\left[\begin{matrix}\delta x_t\\ \delta u_t \end{matrix}\right]^T \nabla^2_{x_t,u_t} c(\hat{x_t},\hat{u_t})\left[\begin{matrix}\delta x_t\\\delta u_t \end{matrix}\right]+\left[\begin{matrix}\delta x_t\\ \delta u_t\end{matrix}\right]^T \nabla_{x_t,u_t}c(\hat{x_t},\hat{u_t})$$
则,Iterative LQR算法流程可以写为:

仔细观察iLQR算法,我们会发现这个算法与牛顿法很相似,对于一个非线性的目标函数,先对目标函数进行二阶泰勒展开,计算梯度方向,然后更新x,然后如此循环下去。与牛顿法不同,iLQR对目标函数进行二次展开,对于动力学系统只进行一次泰勒展开。如果使用牛顿法(微分动态规划),那么需要对动力学系统也进行二次展开。
