Deep Q-Network 及其变种
之前我们讲到了值函数方法以及Q-learning,这一节我们将使用一些技巧将Q-learning算法能够真正的用起来。
Q-Learning回顾
回顾Q-Learning
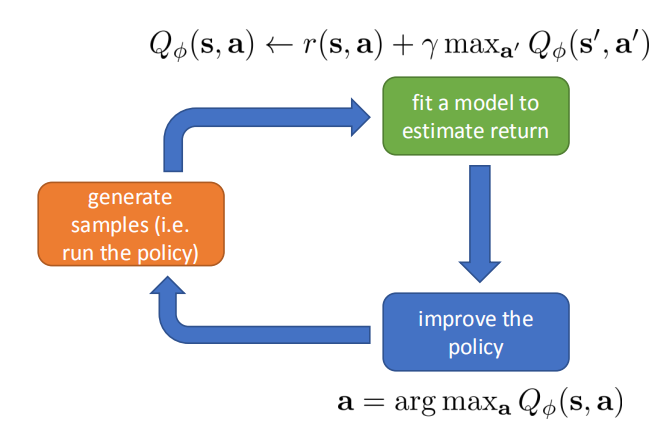
我们先来回顾在值函数方法中提到的Q-Learning算法的大致流程:
- 初始化网络 $Q_{\phi}(s,a)$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$
- 计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_\phi(s’_i,a’_i)$
- 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$,返回 2 直到收敛
流程图如下:
Q-Learning存在的问题
- 在上述算法描述的第4步可以写为:
$$\phi\leftarrow\phi-\sum\nolimits_{i}\alpha\frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-r(s_{i}, a_{i})+\gamma \max _{a^{\prime}} Q_{\phi}\left(s_{i}^{\prime}, a_{i}^{\prime}\right))$$
但在 $r(s_{i}, a_{i})+\gamma \max _{a^{\prime}} Q_{\phi}\left(s_{i}^{\prime}, a_{i}^{\prime}\right)$ 中并没有梯度流通过,因此上述算法的第三步并不是真正的梯度更新,这并不是一个梯度下降算法,所以并不能保证算法的收敛性。 - 此外,算法第 4 步是一个拟合Q值的过程,它应该是一个回归操作,我们注意到这个 $y(s_i,a_i)$ 在迭代过程中一直在变,也就是说我们一直在回归一个变量,这会影响回归的准确性。 - 在算法第 2 步中,使用同一个贪心策略采集的轨迹很可能是相关的,在算法第三步拟合的过程中是在拟合一些具有相关性的样本,拟合效果可能不好。
解决Q-Learning存在的三个问题
使用 Replay Buffers
对于第三个问题,与 AC 算法中一样,我们可以使用同步并行或者异步并行来增加每一批所采集样本的随机性。但对于 Q-Learning 来说还有更好的办法。我们可以使用一个缓冲池来存之前已经采集的 $\{s_i,a_i,r_i,s’_{i}\}$,然后在训练 Q 网络的时候从这个 buffer 抽取一部分进行训练即可。此处,要注意到 Q-Learning 是一个 off-policy 算法,它的策略是来源于 Q 网络,因此训练 Q 网络时,Q 网络并不在意训练样本来自哪一个策略。
因此,带有 replay buffers 的 DQN 算法如下:
- 初始化网络 $Q_{\phi}(s,a)$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$ a. 从 $\mathcal{B}$中采集一个 batch,$\{s_i,a_i,r_i,s’_{i}\} $,令 $n=0$ b. 计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_\phi(s’_i,a’_i)$ c. 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$,若 $n==N$,返回 2 否则返回 a。
使用 Target 网络
下面再来解决回归时目标一直在变化的问题,如果我们能使用另一个 Q 网络,这个网络不经常更新,在计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_\phi(s’_i,a’_i)$ 时使用这个不经常更新的 Q 网络,那么回归目标一直在变的问题就会得到解决。此外,在迭代时梯度不准确的问题也解决了。
使用target网络,并且带有replay buffer的DQN算法如下:
- 初始化网络 $Q_{\phi}(s,a),Q_{\phi’}(s,a)$
- 保存 target 网络的参数:$\phi{‘} \leftarrow \phi$ i. 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$ a. 从 $\mathcal{B}$ 中采集一个batch,$\{s_i,a_i,r_i,s’_{i}\}$ b. 计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$ c. 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$,嵌套内循环循环几次是超参数,可以自行定义。
注意到上面算法的第 b 步中,是使用 $Q_{\phi{‘}}$ 来计算 $\gamma\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$ 的。
DQN及其变种
经典DQN
现在我们给出经典DQN算法:
- 初始化网络 $Q_{\phi}(s,a), Q_{\phi’}(s,a)$, $Q_{\phi}(s,a), Q_{\phi’}(s,a)$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$,$n\leftarrow 0$
- 从 $\mathcal{B}$ 中采集一个batch,$\{s_i,a_i,r_i,s’_{i}\}$
- 使用target网络计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$
- 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$
- $n\leftarrow n+1$,如果$n==N$,更新$\phi’$,回到 2
继续改进
注意到我们每循环 $N$ 次才更新 $\phi’$,那么在总循环第 $N+1$ 次和循环 $2*N-1$ 次的时候都是用的老的 $\phi’$,第 $2*N$ 次循环时又立刻变成了新的 $\phi’$。在这两次相邻的迭代过程中,$\phi’$ 产生了突变,从直觉上来看这种情况并不好。因此,有人提出了使用类似于Polyak Averaging的更新 $\phi’$ 的方法。公式如下:
$$\phi^{\prime} \leftarrow \tau \phi^{\prime}+(1-\tau) \phi \tag{1}$$
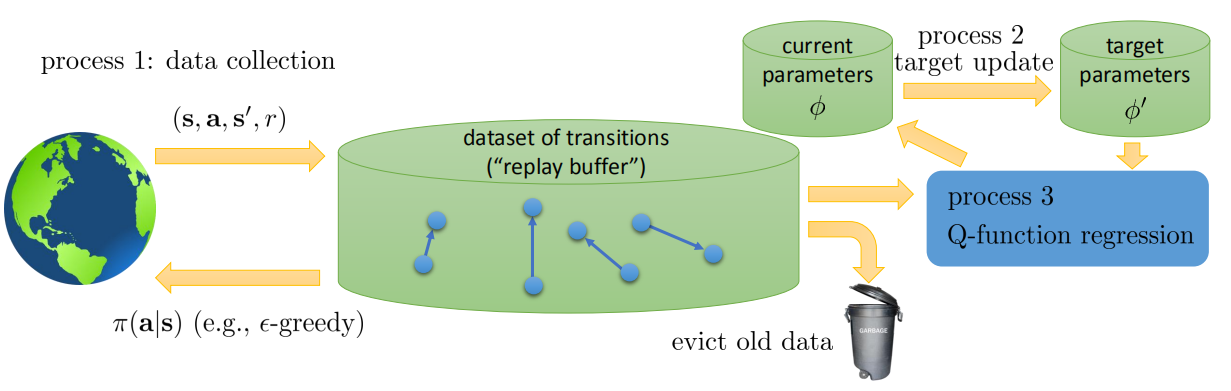
通常来说,$\tau=0.999$ 可以取得较好的效果。在上面经典 DQN 算法中,把第 6 步改成公式(1)即可。下图是 DQN 总体算法图。
Q值准确吗
下面我们先给出经典DQN算法(带target网络、带replay buffer、带Polyak Averaging):
- 初始化网络 $Q_{\phi}(s,a),Q_{\phi’}(s,a)$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$,$n\leftarrow 0$
- 从 $\mathcal{B}$ 中采集一个batch,$\{s_i,a_i,r_i,s’_{i}\}$
- 使用 target 网络计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$
- 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$
- $n\leftarrow n+1$,如果$n==N$,更新$\phi^{\prime} \leftarrow \tau \phi^{\prime}+(1-\tau) \phi, \quad \tau=0.999$,回到 2
但是通过这种算法得到Q网络通常会过分的估计Q值,即网络预测出来的Q值通常比真实的Q值要大。下图是DQN估计的Q值,以及真实的Q值的对比。
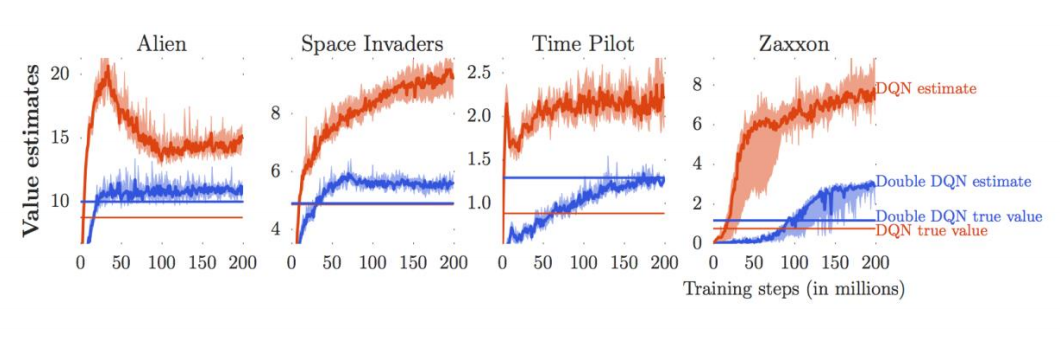
Q 网络过分估计 Q 值的原因在于 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$ 这个式子中取 $\max$ 的步骤,如果 $Q_{\phi{‘}}(s’_i,a’_i)$ 中噪声很大,取 $\max$ 的步骤会把噪声中的最大值也算进去,从而使迭代过程中Q值的估计越来越大。注意到,$\max_{a’}Q_{\phi{‘}}(s’_i,a’_i)$ 可以写为 $Q_{\phi^{\prime}}\left({s}^{\prime}, \arg \max _{{a}^{\prime}} Q_{\phi^{\prime}}\left({s}^{\prime}, {a}^{\prime}\right)\right)$,其中 $Q_{\phi{‘}}(s’_i,a’_i)$ 噪声很大,同时选择最佳动作时噪声也很大。动作的选择是依据 $Q_{\phi{‘}}$,动作的评估也是依据 $Q_{\phi{‘}}$,那么我们能不能把这两者分开呢?
Double Q-Learning
double Q-Learning 的想法就是尽量在选择动作的网络与评估动作的网络是两个网络,如果这两个网络的误差分布不一样,我们就能缓解过分估计Q值的问题,下面公式给出了 double Q-Learning 的基本思想。
$$Q_{\phi_{A}}({s}, {a}) \leftarrow r+\gamma Q_{\phi_{B}}\left({s}^{\prime}, \arg \max _{{a}^{\prime}} Q_{\phi_{A}}\left({s}^{\prime}, {a}^{\prime}\right)\right)$$
$$Q_{\phi_{B}}({s}, {a}) \leftarrow r+\gamma Q_{\phi_{A}}\left({s}^{\prime}, \arg \max _{{a}^{\prime}} Q_{\phi_{B}}\left({s}^{\prime}, {a}^{\prime}\right)\right)$$
我们完全可以用 target 网络作为第二个Q网络。那么 Double DQN 的算法如下:
- 初始化网络 $Q_{\phi}(s,a),Q_{\phi’}(s,a)$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$,$n\leftarrow 0$
- 从 $\mathcal{B}$ 中采集一个batch,$\{s_i,a_i,r_i,s’_{i}\}$
- 使用 Q 网络和 target 网络计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma Q_{\phi’}\left({s_i}^{\prime}, \arg \max _{{a}^{\prime}} Q_{\phi}\left({s_i}^{\prime}, {a}^{\prime}\right)\right)$
- 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$
- $n\leftarrow n+1$,如果 $n==N$,更新 $\phi^{\prime} \leftarrow \tau \phi^{\prime}+(1-\tau) \phi, \quad \tau=0.999$,回到2
在 4 中我们用 target 网络去评估 Q 值,用当前网络去挑选最佳动作。
Dueling DQN
看这个:我是链接
在连续动作空间中使用Q-Learning
由于在 Q-Learning 中策略是根据计算 $\max_{a}Q_{\phi}(s,a)$ 得到的,当状态空间是离散的时候,这很好解决:一个一个算找到最大值就行了。当状态空间是连续的时候,最直观的想法是通过优化方法找到最大的动作,但这样就会很慢,每一步都要进行一次优化。但我们有更好的解决办法。下面给出当前比较流行的方法 DDPG[1]。DDPG 的想法就是构建另一个网络 $\mu_{\theta}({s})$ 用来得到最佳动作:$\mu_{\theta}({s}) \approx \arg \max _{{a}} Q_{\phi}({s}, {a})$。注意到:$\frac{d Q_{\phi}}{d \theta}=\frac{d {a}}{d \theta} \frac{d Q_{\phi}}{d {a}}$。下面直接看算法流程,很好理解:
- 初始化四个网络:$Q_{\phi},Q_{\phi’},\mu_{\theta},\mu_{\theta’}$
- 使用贪心策略采集一些轨迹 $\{s_i,a_i,r_i,s’_{i}\}$,并把这些轨迹加入 buffer-$\mathcal{B}$,令$n=0$
- 从 $\mathcal{B}$ 中采集一个batch,$\{s_i,a_i,r_i,s’_{i}\}$
- 使用 target 网络 $Q_{\phi’}$ 和 $\mu_{\theta’}({s})$ 计算 $y(s_i,a_i)\approx r(s_i,a_i)+\gamma Q_{\phi’}\left({s_i}^{\prime}, \mu_{\theta’}(s’_i)\right)$
- 更新参数 $\phi$,$\phi\leftarrow\phi-\alpha\sum\nolimits_{i} \frac{dQ_\phi(s_i,a_i)}{d\phi}(Q_\phi(s_i,a_i)-y(s_i,a_i))$
- 更新参数 $\theta$,$\theta \leftarrow \theta+\beta \sum\nolimits_{i} \frac{d Q_{\phi} \left({s}_{i}, {a}\right)}{d {a}}\frac{d \mu_\theta \left({s}_{i}\right)}{d \theta}$
- $n\leftarrow n+1$,如果 $n==N$,利用 Polyak Averaging 更新 $\phi^{\prime},\theta’$,回到 2
一些技巧
- 在你写完DQN的时候,先让你的算法在一些简单的强化学习环境中跑跑,成功了说明代码没问题。
- 大的 replay buffer 有助于增强算法的稳定性。
- DQN 刚开始训练的时候很随机,需要耐性等待。
- 使用贪心策略的时候,刚开始 $\epsilon$ 可以调大一些。
- 使用 Double Q-Learning 通常效果改善很多。
- 使用可变学习率的优化器例如 Adam 会比较好。
- 用不同的随机数种子试试。
- 贝尔曼残差的梯度可能会很大,可以截断梯度,或者使用 huber loss
- N 步回报也值得一试
