Actor-Critic 算法
改进策略梯度方法
使用reward-to-go的期望
之前提到了策略梯度法(on-policy, no baselines, causality的策略梯度),算法流程大致为:
- 利用策略$\pi_{\theta}(a|s)$,在环境中交互得到轨迹$\{\tau^i\}$
- 根据公式(1)计算这一批轨迹的$\nabla_\theta J(\theta)$
- 使用梯度上升更新$\theta, \theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$,并回到i
其中$\nabla_{\theta}J(\theta)$为:
$$\begin{align} \nabla_\theta J(\theta) &\approx\frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t}) \biggl( \sum_{t’= t}^Tr(s_{i,t’},a_{i,t’}) \biggr) \\ &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})\hat{Q}_{i,t} \end{align} \tag{1} $$
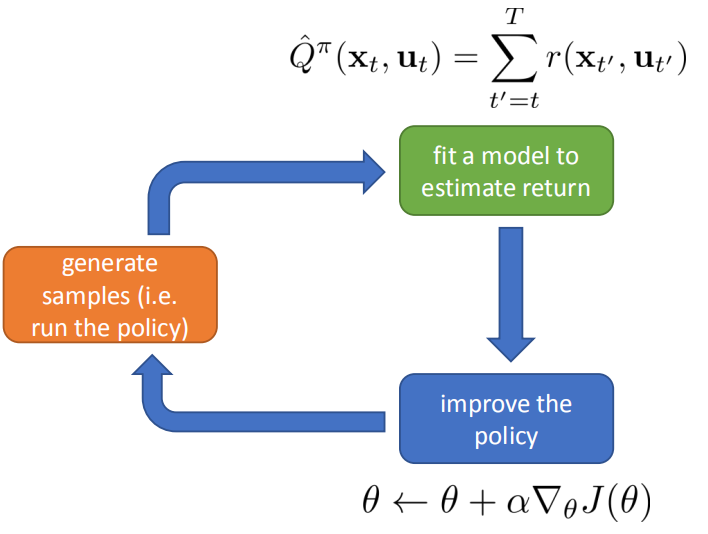
公式(1)中的$\hat{Q}_{i,t}$是轨迹$i$在时刻$t$之后的累计回报(暂时不考虑折扣因子$\gamma$),这个$\hat{Q}_{i,t}$用于估计在状态$s_{i,t}$的条件下执行动作$a_{i,t}$,得到的累计回报。显然,如果仅仅使用轨迹$i$的数据来估计不太准确,方差很大。我们是否能使用真实的reward-to-go去代替这个$\hat{Q}_{i,t}$呢,也就是使用在状态$s_{i,t}$执行动作$a_{i,t}$后的平均累计回报值?当然可以,那使用真实期望$Q^\pi(s_t,a_t)=\sum_{t’=t}^T E_{\pi_\theta}\bigl[r(s_{t’},a_{t’})|s_t,a_t\bigr]$去代替$\hat{Q}_{i,t}$就行了,显然,这么做会更加准确。因此,公式(1)可以改为:
$$\begin{aligned} \nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})Q^\pi(s_{i,t},a_{i,t}) \end{aligned} \tag{2}$$
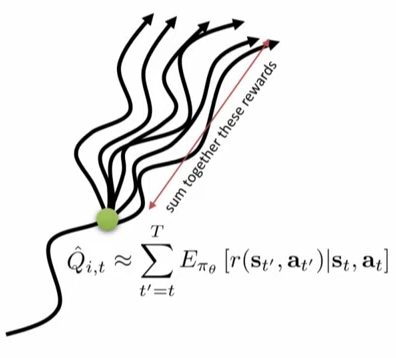
然而,如何求$Q(s_t,a_t)$呢?你可以在某条轨迹的某条状态下,多次的执行同一个策略得到多条轨迹分支来估计这个值,如下图所示。
使用优势函数
在策略梯度法里说过使用baseline可以降低策略梯度法的方差,这个baseline可以有多种形式,它可以是一个常量(所有轨迹的累计回报的平均值),也可以是状态-值函数$V^\pi(s_t)=E_{a_t\sim\pi_\theta(a_t|s_t)}[Q(s_t,a_t)]$。那么公式(2)可以改写为:
$$\begin{align} \nabla_\theta J(\theta) &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})\big(Q^\pi(s_{i,t},a_{i,t})-V^\pi(s_{i,t})\big) \\ &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})A^\pi(s_{i,t},a_{i,t}) \end{align} \tag{3}$$
公式(3)中$A(s_{i,t},a_{i,t})$被称之为优势函数,意味着在状态$s_{i,t}$下,执行动作$a_{i,t}$后得到的累计回报会比平均值多多少。
由于$Q^\pi(s_{i,t},a_{i,t})\approx r(s_t,a_t)+V^\pi(s_{t+1})$,因此公式(3)可以写为:
$$\begin{aligned} \nabla_\theta J(\theta) &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})\big(r(s_{i,t},a_{i,t})+V^\pi(s_{i,t+1})-V^\pi(s_{i,t})\big) \end{aligned} \tag{4}$$
其中优势函数为:
$$\begin{align} A^\pi(s_{i,t},a_{i,t})=r(s_{i,t},a_{i,t})+V^\pi(s_{i,t+1})-V^\pi(s_{i,t}) \end{align} \tag{5}$$
根据公式(4)我们可以知道,只需要能估计出$V(s_t)$,我们就能计算$A(s_t,a_t)$了。
估计优势函数/值函数
我们知道值函数$V(s)$的定义是:智能体在状态$s$的情况下利用策略$\pi$与环境交互,$V(s)$是从状态$s$起得到的累计回报的均值。因此,如果我们要使用神经网络去估计$V^\pi(s_t)$,那么可以在利用智能体采集到一条轨迹后,就计算这条轨迹中每个状态的累计回报,得到多个状态-累计回报对$\{(s_{i,t},\sum_{t’=t}^{T}r(s_{i,t’},a_{i,t’}))\}$,利用这些状态-累计回报对和MSE损失去训练神经网络,得到一个好的值函数$V(s_t)$的估计器。
在实践中有一种低方差的trick去训练$V(s_t)$,训练数据的格式为:$\{(s_{i,t},r(s_{i,t},a_{i,t})+\hat{V}_{\phi}^\pi(s_{i,t+1}))\}$,此处$\hat{V}_{\phi}^\pi(s_{i,t+1}))$为之前的值函数的估计值。这种训练值函数的方法称之为”bootstrapped 估计”。上一段使用状态-累计回报对$\{(s_{i,t},\sum_{t’=t}^{T}r(s_{i,t’},a_{i,t’}))\}$的方法称之为“蒙特卡洛估计”。
Actor-Critic算法
下面导出Actor-Critic算法:
- 随机初始化一个策略网络$\pi_\theta(a|s)$和值函数网络$\hat{V}_{\phi}^\pi(s)$
- 利用策略$\pi_{\theta}(a|s)$在环境中交互得到一个状态-动作-回报对$\{s_{i,t},a_{i,t},r(s_{i,t},a_{i,t})\}$
- 利用$\{(s_{i,t},r(s_{i,t},a_{i,t})+\hat{V}_{\phi}^\pi(s_{i,t+1}))\}$作为训练数据去训练$\hat{V}_{\phi}^\pi(s)$
- 利用公式(4)得到$\nabla_\theta J(\theta)$
- 利用梯度法对$J(\theta)$ 进行优化:$\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$,得到新的策略$\pi_{\theta}(a|s)$,并返回2
引入折扣因子
引入折扣因子$\gamma$的直觉是:我们总是认为当前的回报要比未来的回报重要,同时也避免累计回报变为无穷大的局面。引入折扣因子后,累计回报被定义为:
$$r(\tau)=\sum_{t=1}^T r(s_t,a_t) \tag{6}$$
公式(1)(on-policy, no baselines, causality的策略梯度)就被定义为:
$$\begin{aligned} \nabla_\theta J(\theta) &\approx\frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t}) \biggl( \sum_{t’= t}^T \gamma^{t’-t} r(s_{i,t’},a_{i,t’}) \biggr) \end{aligned} \tag{7}$$
使用优势函数的策略梯度为:
$$\begin{aligned} \nabla_\theta J(\theta) &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})\big(r(s_{i,t},a_{i,t})+\gamma V^\pi(s_{i,t+1})-V^\pi(s_{i,t})\big) \end{aligned} \tag{8}$$
带折扣因子的Actor-Critic方法
下面根据公式(8)得到带折扣因子的Actor-Critic方法:
- 随机初始化一个策略网络$\pi_\theta(a|s)$和值函数网络$\hat{V}_{\phi}^\pi(s)$
- 利用策略$\pi_{\theta}(a|s)$ 在环境中交互得到状态-动作-回报对 $\{s_{i,t},a_{i,t},r(s_{i,t},a_{i,t})\}$
- 利用$\{(s_{i,t},r(s_{i,t},a_{i,t})+\hat{V}_{\phi}^\pi(s_{i,t+1}))\}$, 作为训练数据去训练$\hat{V}_{\phi}^\pi(s)$
- 利用公式(8)得到$\nabla_\theta J(\theta)$
- 利用梯度法对$J(\theta)$进行优化:$\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$,得到新的策略$\pi_{\theta}(a|s)$,并返回2
注意上述AC算法是批量更新,即采集一些轨迹后再更新策略网络和值函数评估网络。这个方法可以用于在线版本,即得到一个状态-动作-回报对以后就可以更新,但通常来说不推荐使用On-line版本的AC算法,因为通常来说很难训练,即使在监督学习中我们也不推荐一个样本一个样本的更新。
Actor与Critic共享权重
在实际应用Actor-Critic算法的过程中,通常而言我们会使用两个网络:一个策略网络输出策略、一个值函数估计网络估计值函数。但是,我们注意到这两个网络的输入都是状态$s$,因此这两个网络的最初几层的权重可能具有一定的相似性。所以,我们可以让这两个网络共享权重,使我们在训练过程中收敛速度更快。
并行Online-Actor-Critic算法
上面说到online版本的Actor-Critic算法由于每次训练时只有一个样本,因此会导致方差很大。但Online版本的算法又格外优雅,为了更好的使用Online版本算法,我们通常会使用同步并行机制或异步并行机制,增加每次更新的batch size,从而实现Online版本的Actor-Critic算法。
下面首先给出基本的Online Actor-Critic算法流程:
- 随机初始化一个策略网络$\pi_\theta(a|s)$和值函数网络$\hat{V}_{\phi}^\pi(s)$
- 利用策略$\pi_{\theta}(a|s)$,在当前状态下执行动作$a$一个状态-动作-回报对$\{s,a,r(s,a),s’\}$
- 利用$\{(s,r(s,a)+\hat{V}_{\phi}^\pi(s’))\}$作为训练数据去训练$\hat{V}_{\phi}^\pi(s)$
- 计算advantage,$\hat{A}^\pi(s,a)=r(s,a)+\gamma\hat{V}_{\phi}^\pi(s’)-\hat{V}_{\phi}^\pi(s)$
- $\nabla_\theta J(\theta)\approx\nabla_\theta \log \pi_{\theta}(a|s)\hat{A}^\pi(s,a)$
- 利用梯度法对$J(\theta)$进行优化:$\theta\leftarrow\theta+\alpha\nabla_\theta J(\theta)$,得到新的策略$\pi_{\theta}(a|s)$,并返回2
同步并行
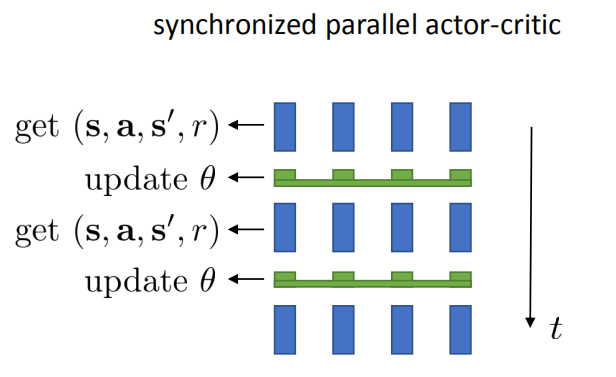
由于在上述算法的第五步中,只用了一个样本计算梯度,导致梯度方向不是很准确,因此我们的目的是使用多个样本来训练。对于同步并行机制来说,就是在算法第二步中同时在多个环境中使用相同的策略进行交互(下图中为4个),在每个环境都得到一个$\{s,a,r(s,a),s’\}$,然后把这四个$\{s,a,r(s,a),s’\}$一起训练,解决梯度方向不太准确的问题。其机制如下图所示。
异步并行
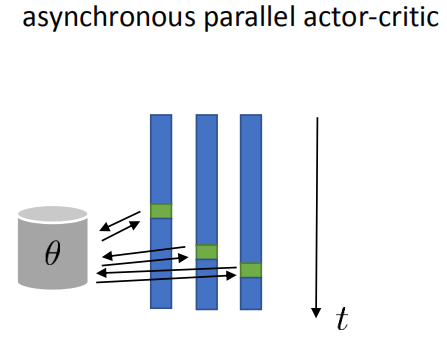
异步并行与同步并行相同,它也是让智能体在多个环境交互。不同之处在于在异步并行中,在某一时刻每个智能体在环境中交互的步长不同,有些可能已经执行了10步,有些可能此时已经执行了20步。但他们在更新策略时都是使用的同一个策略网络。其机制如下图所示。异步并行的好处是代码实现简单。有人提出的A3C算法就是基于这种机制。
Actor-Critic or Policy Gradient
我们现在来看看actor-critic方法与policy gradient方法的区别。
Policy Gradient
带baseline与考虑因果性的policy gradient的目标函数的梯度如下:
$$\begin{aligned} \nabla_\theta J(\theta) &\approx\frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t}) \biggl( \sum_{t’= t}^T \gamma^{t’-t} r(s_{i,t’},a_{i,t’}) -b \biggr) \end{aligned} \tag{9}$$
其特点为:对累计回报值的估计为无偏估计,但方差比较大,这是因为每次只用这一条轨迹的累计回报去评估当前动作的好坏。
Actor-Critic
Actor-Critic的目标函数的梯度如下:
$$\begin{aligned} \nabla_\theta J(\theta) &\approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t})\big(r(s_{i,t},a_{i,t})+\gamma V^\pi(s_{i,t+1})-V^\pi(s_{i,t})\big) \end{aligned} \tag{10}$$
其特点为:低方差,但当Critic不够好的时候对累计回报值的估计不是无偏估计。
使用值函数估计代替b
Policy Gradient的特点是对目标函数的估计是无偏估计,但方差大;Actor-Critic的特点是方差低但不是无偏估计,我们能不能想一种既方差小又是无偏估计的目标函数呢?答案是肯定的,注意到在Policy Gradient那一章中,我们已经证明了在$J(\theta)$中减去任意的常量b都是无偏的,那么我们可以将$b$更改为$\hat{V}_{\phi}^\pi(s_{i,t})$,这是因为累积回报的期望本来就是$V^\pi(s)$,让它减去它的均值就能让它的梯度更加准确。因此,目标函数的梯度可改写为:
$$ \begin{aligned} \nabla_\theta J(\theta) &\approx\frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T\nabla_\theta\log \pi_\theta(a_{i,t}|s_{i,t}) \biggl( \biggl(\sum_{t’= t}^T \gamma^{t’-t} r(s_{i,t’},a_{i,t’})\biggr) - \hat{V}_{\phi}^\pi(s_{i,t}) \biggr) \end{aligned} \tag{11} $$
利用值函数估计来代替baseline的算法称之为 Vanilla Policy Gradient.
改进优势函数的两种方法
n步回报
公式(11)中利用值函数网络去估计值函数,并将其作为baseline来减少方差,但是这个方差依然不让人满意,不让人满意的地方在于:在训练中后期,用值函数去估计累计回报是非常有效的减少方差的方式(公式10), 在训练前期可以适当使用轨迹中多步累计回报来近似平均累计回报(公式11)。结合这两者,有人提出了下面的advantage公式:
$$\hat{A}_n^\pi(s_t,a_t)=\bigg(\sum_{t’=t}^{t+n}\gamma^{t’-t}r(s_{t’},a_{t’}) \biggr)-\hat{V}^\pi_\phi(s_t)+\gamma^{n}\hat{V}^\pi_\phi(s_{t+n})$$
这个Advantage公式被称之为n步回报。
Generalized Advantage Estimation(GAE)
基于n步回报,有人又提出了以下公式:
$$\begin{aligned} \hat{A}_{GAE}^\pi(s_t,a_t)&=\sum_{n=1}^{\infty}w_n\hat{A}_n^\pi(s_t,a_t), \quad w_n =\lambda^{n-1} \\ &=\sum_{t’=t}^{\infty}(\gamma\lambda)^{t’-t}\delta_{t’}, \quad \delta_{t’}=r(s_{t’},a_{t’})+\gamma\hat{V}^\pi_\phi(s_{t’+1})-\hat{V}^\pi_\phi(s_{t’}) \end{aligned} $$
目前来说,GAE比较好用,用得也非常广泛,几乎大部分强化学习库都实现了GAE
